Альберт Эйнштейн однажды сказал: «Никто не может выиграть в рулетку, если он не крадет деньги со стола, пока крупье не смотрит».
Пусть обычно я не задаю вопросов Эйнштейну, это утверждение неверное. Вы можете использовать преимущество при играх в казино под названием – "физика". Ластплей поможет вам правильно вести себя в казино и расскажет все его тонкости. Так, а пока что вернемся к Эйнштейну.
На самом деле Эйнштейн имел в виду, что нет никакого математического трюка, который может помочь вам выиграть в рулетку. Физика даёт небольшое преимущество, но здесь все зависит от удачи и последовательности ставок на определенные числа. Каждый спин – это независимое испытание. Это отличается от такой игры, как Блэкджек, где вероятности меняются по мере раздачи карт.
Но некоторые считают, что можно использовать то, как крутится рулетка и сделать примерное вычисление того, какое число выпадет.
Идея заключается в том, что вы можете делать ставки на макет таким образом, что вы гарантированно выиграете. Но возможно ли это на самом деле?
Подобно мишени для игры в «Дартс» расположение рулеточного колеса не возникло случайно. Он был тщательно спланирован и обладает определенными свойствами. На самом деле, есть два разных макета. Американское колесо и Европейское колесо. Эти два макета показаны ниже.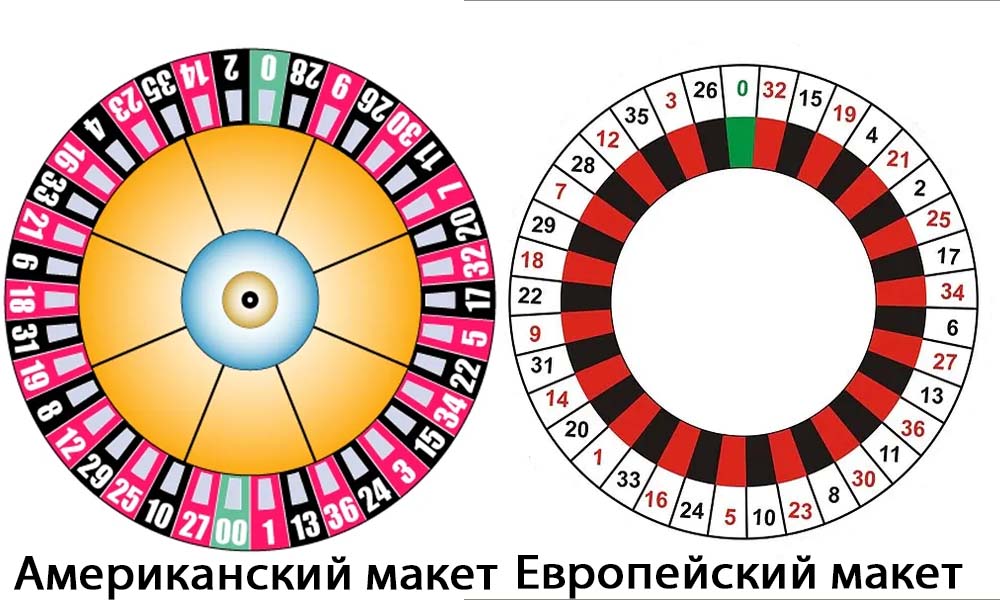
Обратите внимание, что американское колесо имеет два нуля. Это важно, так как это удваивает преимущество для казино. На европейском колесе вы бы потеряли, в долгосрочной перспективе, 2.7% от любых денег, на которые ставите. На американском колесе вы потеряете 5,26%.
Номера расположены в различном порядке на каждом колесе, но есть некоторые сходства в шаблонах. На обоих колесах красные и черные числа чередуются вокруг колеса, хотя если вы уберете нули, американское колесо будет иметь последовательные красные и черные цвета. Колеса также структурированы таким образом, что низкие числа (1-18) и высокие числа (19-36) должны чередоваться как можно больше.
Именно по этой причине американское колесо считается не столь сбалансированным, как европейское. Оба колеса также стараются распределить нечетные и четные числа как можно более равномерно.
На европейском колесе есть еще две интересные симметрии. Во-первых, все низкие красные числа и черные высокие числа находятся на одной стороне нуля, а высокие красные числа и низкие черные числа-на другой стороне. Во-вторых, последовательность 29-7-28-12-35-3-26-0-32 не содержит чисел между 13 и 24 (вторая дюжина). Так, например, вы можете сделать ставку на всю вторую дюжину, с коэффициентом 2.1%.
Итак, как же математика поможет выиграть в рулетку?
Математическая система должна быть построена путем комбинаций игровых стратегий, подбора чисел и управления капиталом. Пожалуй, самая известная стратегия управления капиталом - это система Мартингейла. Эта система гарантированно подарит вам деньги, пока у вас достаточно банкроллов, чтобы удваивать свою ставку после выигрыша. Но тут есть огромный минус, именно система Мартингейла, вероятно, является самым быстрым способом банкротства, известным человеку.
Так что математика и физика увы не помощники. Нет никакой вероятности, что-то число, на которое вы поставили раньше и выиграли, повторит такую же судьбу и в этот раз. Несомненно, любая система может быть проанализирована, дабы показать вам уязвимые места рулетки. Но как правило казино – это вещь в котором господствует госпожа Удача.
Понравилась статья? Поделитесь ею в социальных сетях!














